One of the most important applications of Python programming is in the area of mathematics. Python is highly equipped with numeric types and operations that allow coders to carry out math operations with their data.

However, some mathematical operations are complex and can be tedious to code. One such operation is the LCM (Least Common Multiple). Fortunately, Python provides us with a convenient way to do this operation without having to code it ourselves.

In this article, we will discuss the math.lcm function provided by Python, show examples of how to make use of it and use the lcm function to write code that adds two or more functions together. Let’s begin.

The Lowest Common Multiple (LCM) in Mathematics

Before we explore how to make use of math.lcm function, we need to first understand the related math concept of the LCM (Least/Lowest Common Multiple). The LCM of two numbers, let us call them x and y, is another number that is the smallest of all the multiples that are common to x and y.

For example, say we had two whole numbers 12 and 18, let us first list out their individual multiples:

• 12= 12, 24, 36, 48, 60, 72, …
• 18= 18, 36, 54, 72, 90, 108, …

The multiples that are common to 12, and 18 are in bold, that is, 36, 72, …

The smallest multiple common to both 12 and 18 is 36.

I hope you get the concept.

There are several methods of computing the LCM manually, but that is beyond the scope of this article. Our concern is how to make use of Python math.lcm to automate the process for us. This is what we want to touch on in the next section.

Understanding math.lcm in Python

Python’s math module has a repertoire of mathematical functions that can make our computations much simpler. One of the functions it provides is the lcm function which gets the LCM of two or more whole numbers.

In order to make use of lcm function, we need to make sure that your Python version is at least 3.9. Then, we will have to import the math module. The general usage is as follows:

import math

lcm_result = math.lcm(number1, number2, ...)

Here, number1, number2, and so on are the integer numbers we want to find the LCM of. math.lcm is highly flexible, since we can pass in any number of arguments. This will allow us to find the LCM of even more than two numbers.

For the return values, we have the following scenarios:

• If math.lcm is called with all arguments equal 0, it will return 0.
• If math.lcm has zero arguments, it will return 1
• If a non-integer value (like a float or str) is passed into the function, math.lcm will raise a TypeError

First example: LCM of two numbers

We shall try to make use of Python’s math.lcmto find the LCM of two numbers. The code below illustrates this.

import math

num1 = 12
num2 = 18

lcm_result = math.lcm(num1, num2)

print(f"The LCM of {num1} and {num2} is: {lcm_result}")

We are making use of math.lcm to calculate the LCM of 12 and 18, the numbers we made use of in our previous explanation. When the code is executed, we get the following output:

Another Example: Find the LCM of three numbers

This next example will show how to find the LCM of 4, 6, and 8 using Python’s math.lcm.

import math

num1 = 4
num2 = 6
num3 = 8

lcm_result = math.lcm(num1, num2, num3)

print(f"The LCM of {num1}, {num2}, and {num3} is: {lcm_result}")

The code in this example is similar to the previous one, but we are computing the LCM of 4, 6, and 8. The output is as expected (see the below figure):

Applications of LCM: Simplifying Common Fractions

The concept of LCM in mathematics has several applications. One of the most common applications is adding/subtracting two or more common fractions. For example, we might want to simplify the following expression:

Since the denominators are not common, we will need to make use of the LCM of the denominators to convert each of the fractions into equivalent forms having common denominators. That is, since the LCM of 3 and 6 is 6, we can do the following:

• For the first fraction, divide the LCM by the denominator 3, to get 2, then multiply both the numerator and denominator by 2. That is:

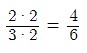
• For the second fraction, divide the LCM by the denominator 6, to get 1, then multiply both the numerator and denominator by 1. That is:

• Now that both converted fractions have the same denominator (thank you LCM!), we can now proceed to add them both:

Python code to Add or Subtract Common Fractions

We now want to implement Python code that will help us simplify common fractions. The expression will be given as a string value. For example, "2/3+1/6", and the returned result will be a string also.

For now, only addition operations will be supported to make the code easier, but you are free to extend the code to support subtraction too.

First, we have to import the math module to make sure we can make use of lcm and gcd later. Then next have the following function to parse a single fraction from the string into a tuple for easy handling:

def parse_fraction(str_frac):
    try:
        if "/" in str_frac:
            num, den = str_frac.split("/")
            num = int(num)
            den = int(den)

        else:
            num = int(str_frac)
            den = 1

        return num, den
    
    except:
        raise ValueError(f"fraction '{str_frac}' is not a valid fraction")

This function parse_functionsplits the string at the division character /. This helps us store the numerator and denominator as separate integers. if there’s no division character, the fraction is created with a denominator of 1.

We next implement the function, reduce, to help reduce a fraction to the lowest terms. The code snippet is shown below:

def reduce(fraction):
    num, den = fraction
    
    gcd = math.gcd(num, den)
    num //= gcd
    den //= gcd

    return num, den

The function makes use of the gcd (see how useful the mathmodule is?) to carry out a reduction to the lowest terms.

Moving on, we next need to convert our fraction tuple into a string representation using the fraction_to_str function. This will prevent us from having an unreadable result. See the code snippet below:

def fraction_to_str(fraction):
    num, den = fraction

    if den==1:
        return str(num)
    
    return f"{num}/{den}"

Finally, we need a function that simplifies the fraction expression. All the fractions should be added up, no subtraction is allowed (as mentioned earlier). The function for this is add_fractions, that it accepts the expression to simplify as a string.

def add_fractions(str_expr):
    fractions = str_expr.split("+")
    result_num = 0
    result_den = 1

    for fraction in fractions:
        num, den = parse_fraction(fraction)
        lcm = math.lcm(result_den, den)

        # get the result numerator and the result denominator
        result_num = result_num * (lcm // result_den) + num * (lcm // den)
        result_den = lcm

    return fraction_to_str(reduce((result_num, result_den)))

The add_fractionsfunction makes use of all the previous functions we defined to successfully simplify the fraction sum (in the string parameter).

That’s just about it. We now have a simple Python code to help us add two or more common fractions. Sample usage is as follows:

print(add_fractions("1/2+1/2"))        # outputs 1
print(add_fractions("1/3+1/3+1/3"))    # outputs 1
print(add_fractions("2/3+1/6"))        # outputs 5/6
print(add_fractions("3/4+1/6"))        # outputs 11/12

The comments show the corresponding outputs for each call to add_fractions.

We have successfully made use of the math.lcm to create a function to add fractions. The code can be extended in any way you want. for example

• The fractions could become a Fraction object.
• The function add_fractionscould become an __add__ method.
• A __sub__method could be added to support subtraction.
• The function reducecould be made into a method that helps reduce a Fractionobject to lowest terms.

The least common multiple (LCM) is a fundamental concept in mathematics and is used in various scenarios, for example adding and subtracting fractions.

Python has provided the lcm function in the math module to make it easy to calculate the LCM of two or more whole numbers. We have also implemented a simple Python code that demonstrates the usefulness of math.lcm helping us add common fractions together.

If you enjoyed this tutorial, please check out our knowledgebase for more tutorials like this one on Python programming that will help you in your coding journey. Meanwhile, have fun coding!